introduction to algorithms notes6

＜Introduction to algorithms＞笔记

Part7 高级算法问题

在part1-6学习基本的数据结构和算法问题后, part7不再集中于对一个算法问题专题进行学习, 而是就不同的高级算法问题进行基本的介绍,其其覆盖的内容十分全面,涉及一下几个领域:

• 排序网络
• 矩阵运算
• 线性规划
• 字符串匹配

Chapter26 如何利用多核来并行排序?

在part2中学习了基本的排序算法,包括插入,快排,归并,堆排序等,它们都是在串行计算机上线性执行的算法.随着硬件的发展,多处理器的进步,如何利用多核来进行并行排序?如何推而广之到多核并行算法?这一章就套路基于计算的一种比较网络模型,同时进行多个比较操作.

比较网络与串行排序算法的区别:

• 比较网络只能执行比较操作, 即只能执行基于比较操作的算法.因此part2中学习的计数排序就无法再比较网络中实现
• 比较网络中比较操作可以并行的执行, 而串行排序算法各操作是依次执行的.故前者拥有更好的算法效率- 更小的算法复杂度

1.比较网络定义

• 组成：
  基本构件:线路和比较器
  

• 比较网络含义：
• 一个由线路互相联接着的比较器的集合,我们把具有n个输入的比较网络画成一个由n条水平线组成的图,比较器则垂直地与两条水平线相连接.每个比较器的输入端要么与网络的n条输入线路 $a_1,a_2, \dots, a_n$ 中的一条相连,要么与另一个比较器的输出端相连接.类似地,每个比较器的输出端要么与网络的n条输出线路 $b_1,b_2, \dots, b_n$中的一条相连,要么与另一个比较器的输入端相连接.互相连接的比较器主要应满足如下要求：

  1. 其互相连接所成的图中必须没有回路.
  2. 只有当同时有两个输入时,比较器才能产生输出值.

在每个比较器均运行单位时间的假设下,我们可以对比较网络的“运行时间”作出定义,这就是从输入线路接收到其值的时刻到所有输出线路收到其值所花费的时间.

• 比较网络示意图:
  

• 排序网络定义:
  对每个输入序列其输出序列均为单调递增(即 $b_1 \leq
  b_2, \dots, b_n$ )的一种比较网络

• 0-1原理：
  如果一个具有n个输入的比较网络,能够对所有可能存在的2^n个0和1组成的序列进行正确的排序,则对所有任意数组成的序列,该比较网络也可能对其正确排序.
  0-1原理推定认为：如果对于属于集合{0,1}的每个输入值,排序网络都能正确运行,则对任意输入值,它也能争取而运行(输入值可以是整数、实数或者任意线性排序的值的集合).这样在构造排序网络时,可以专注在0和1组成的输入序列上设计比较器.这个原理目的是简化输入值,而通过0和1来设计比较网络的线路和比较器,只要0和1可运行,那么其他任意值的序列也都可以运行.
  0-1原理的证明依赖单调递增函数.如果比较网络把输入序列 $a=<a_1,a_2, \dots, a_n>$ 转化为输出序列 $b=<b_1,b_2, \dots, b_n>$,则对任意单调递增函数f,该网络把输入序列f(a)=<f(a1),f(a2),…,f(an)>转化为输出序列f(b)=<f(b1),f(b2),…,f(bn)>.
  这个可以这样理解,对输入序列a施以f(a)单调递增函数,比较网络(线路和比较器)能够使序列a输出序列b,那么该比较网络同样可以使输入序列f(a)输出序列f(b).
  这就为0-1原理奠定了基础,只要证明比较网络可以运行于0和1的输入,那么设计一个单调递增函数,0和1是因变量,其自变量自然也可以通过同样比较网络来排序.
  如果一个具有n个输入的比较网络能够对所有可能存在的2n个0和1组成的序列进行正确的排序,则对所有任意数组成的序列,该比较网络也可能对其正确排序.
  0-1原理证明用到了单调递增函数概念,同时采用数学归纳法和反证法来证明.这也给出了一个很重要的思想,那就是对现实问题的解决,在构建数学模型时,可以简单到0-1,然后再推广到复杂数.

• 双调序列：
  序列要么先单调递增然后再单调递减,要么先单调递减然后又单调递增.例如序列<1,4,6,8,3,2>和<9,8,3,2,4,6>都是双调的

2.双调排序网络

• 双调排序程序由 $log_2n$个阶段组成,其中每一个阶段称为一个半清洁器.每个半清洁器是一个深度为1的比较网络,其中输入线I与输入线I+n/2进行比较,I=1,2,…,n/2(这里假设n为偶数).下图即为一个具有8个输入和8个输出的半清洁器(half-cleaner)
  

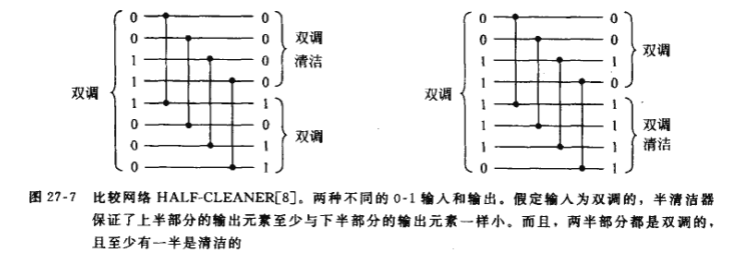
• 当由0和1组成的双调序列用作半清洁器的输入时,半清洁器产生的输出序列满足如下条件：

  1. 较小的值位于输出的上半部,较大的值位于输出的下半部.
  2. 两部分序列仍是双调的.
  3. 两部分序列中至少有一个是清洁的——全由0或1组成.

• 双调排序器(bitonic-sorter)
  通过递归地连接半清洁器,我们可以建立一个双调排序网络.双调排序网络[n]的第一阶段由半清洁器[n]组成,可知半清洁器[n]产生两个规模缩小一半的双调序列且满足上半部分的每个元素不比下半部分的任一个元素大.因此,我们可以运用两个双调排序网络[n/2]分别对两部分递归地进行排序,以此完成整个排序工作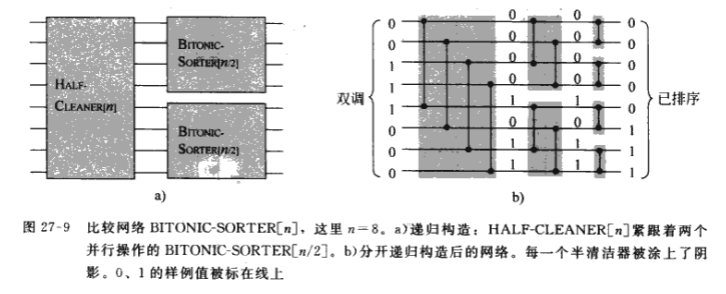
  

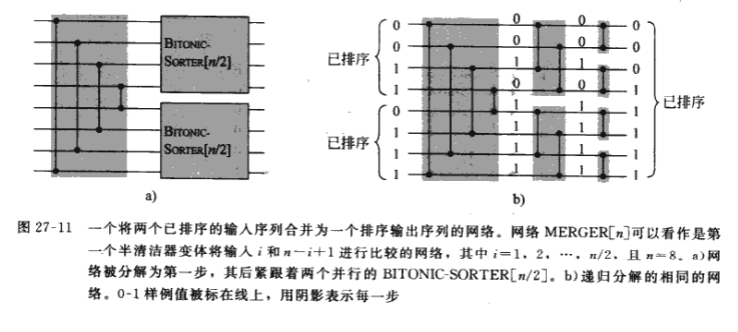
我们只要把含n个元素的双调排序网络的第一个半清洁器修改一下就可以得到合并网络MERGER[n].由于输入的上半部和下半部都是单调递增的,所以我们把比较网络的下半部分颠倒一下,输入就成了一个双调序列.添上半清洁器,再颠倒回去,半清洁器就变成了把输入 $a_i$和$a_{n-i+1}比较.这时,输出也被颠倒了.但是,一个双调序列颠倒了以后还是一个双调序列.
因此就可以用bitonic-sorter对深度为 $\log n$ 的0-1双调序列进行排序.

3.合并网络(mergin network)
合并网络,能够把两个已排序的输入序列合并为一个有序的输出序列的网络.基于双调排序网络思想,对已知的两个有序序列进行连接(第二个序列顺序颠倒),所得的序列是双调序列,再利用双调排序器就能完成两个有序序列的合并.其原理如下:

4.基于0-1原理、双调排序网络、合并网络,我们可以构造一个输入任意序列进行排序的比较排序网络.思想很简单：第一步开展最基础的2个元素的两两比较,这个用普通的比较器就可以实现,输出长度为2的有序序列;第二步对长度为2的有序序列进行两两合并,这个用合并网络排序(基于双调排序器,先连接序列构造双调序列)实现,输出长度为4的有序序列;第三步对长度为4的有序序列进行合并网络,直到 $\log n$次.算法上,可以在 $O(\log n)$内并行地对n个数进行排序.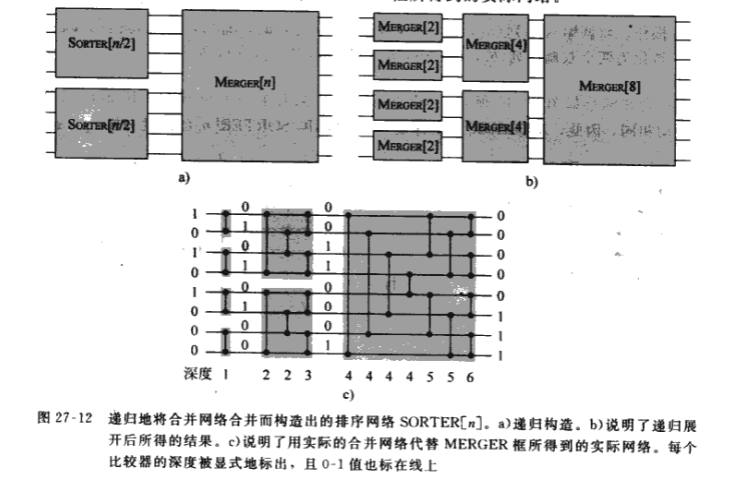

总结:排序网络可以并行地进行排序,然后再组合各并行排序结果,适合分布式场景的排序需求.

Chapter27 矩阵运算

在part4高级设计技术中在动态规划中研究了矩阵链乘法问题后, 这一章深入学习矩阵运算, 特别学习矩阵相乘的Strasssen算法,该算法能在 $O(n^{\log 7})$ 的时间内计算两个 $n*n$ 的矩阵的乘积.

1.首先重温下矩阵的相关概念和性质,为后续矩阵运算奠定数据理论基础.

矩阵A：
数字的一个矩形阵列,形式化为 $A=(a_{ij})$,第i行j列元素为 $a_ij$,如元素为实数的所有元素mXn矩阵组合的元素用 $R_{mXn}$表示.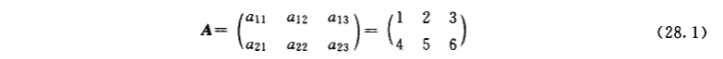

矩阵转置AT：是矩阵A的行和列互相交换而产生的矩阵.

向量(Vector)：是数字的一维向量,列向量看成是nX1的矩阵,转置成行向量就是1Xn的矩阵.

单位向量$e_i$：矩阵第一个元素为1而其他元素均为0的常量.

零矩阵：所有元素都是0的矩阵.

对角矩阵：当i≠j时,$a_ij$,所有非对角线上的元素均为0.

nXn单位矩阵 $I_n$：是对角线元素都是1的对角矩阵.

三对角矩阵T：满足 $|i-j|>1$ 的元素 $t_ij$=0的矩阵,非零元素仅出现在主对角线上、靠主对角线上面和对角线下面.

上三角矩阵U：满足i>j的元素 $U_ij=0$的矩阵,对角线下面的所有元素均为0,若对角线元素为1,则是单位上三角矩阵.

下三角矩阵L：满足i<j的元素 $L_ij=0$的矩阵,对角线上面的所有元素均为0,若对角线元素为1,则是单位下三角矩阵.

置换矩阵P：每一行或列中仅包含一个1,其他元素都为0,可以把一个向量x和一个置换矩阵相乘,结果是向量x中的元素的一种置换.

对称矩阵A：满足条件 $A= A^T$.

矩阵加法：$C(c_ij)=A(a_ij)+B(b_ij),c_ij=a_ij+b_ij$,都是mXn矩阵.

矩阵乘法：相容(A的列数等于B的行数)的两个矩阵才可以相乘,$C(c_ij)= \sum_{k=1}^{m} A(a_ik)*B(b_kj)$,矩阵和单位矩阵等于自己、和零矩阵相乘等于零、和向量相乘得到向量,满足结合律和分配律,但不满足交换律.

逆矩阵A-1：满足 $A A^{-1} = I_n= A^{-1}A$,不可逆的矩阵称为奇异矩阵.

线性相关：设 $x_1,x_2, \dots, x_n$是n个向量,若存在不全为零的常系数 $c_1,c_2, \dots, c_n$,使 $c_1x_1+c_2x_2+ \dots +c_nx_n=0$成立,就称 $x_1,x_2, \dots, x_n$线性相关.

非零mXn矩阵A的秩：A的极大线性无关列向量组中向量的个数为列秩,A的极大线性无关行向量组中向量的个数为列秩.任意一个矩阵的行秩和列秩都是相等.mXn的秩是0和min(m,n)之间的一个整数.

非零mXn矩阵A的秩满足下列条件的最小的数r：存在mXr矩阵B和rXn矩阵C且有A=BC.如果一个nXn的矩阵秩为n,则是满秩,如果一个mXn矩阵的秩为n,则是列满秩.
一个方阵满秩当且仅当它为非奇异矩阵.当前仅当A无空向量时,矩阵A为列满秩.
当且仅当A具有空向量时,方阵A是奇异的.

余子式：对于n>1,nXn矩阵A的第ij个余子式是把A的第i行和第j列元素去掉后所形成的一个(n-1)X(n-1)矩阵A[ij],表示为det(A[ij]).

方阵A的行列式具有如下性质：如果A的任何行或列的元素为0,则det(A)=0;用常如a乘A的行列式任意一行(或任意一列)的诸元素,等于用a乘A的行列式;A的行列式中的一行(或一列)元素加上另一行(或另一列)中的相应元素,行列式的值不变;A的行列式值与其转置矩阵AT的行列式的值相等;行列式的任意两行(或两列)互换,则其值异号.

正定矩阵：nXn矩阵A,如果对所有n维向量x≠0都有$x^TAx>0$,则矩阵A为正定矩阵.

对任意列满秩矩阵A,矩阵$A^TA$是正定的.

2.矩阵乘法的Strassen算法
矩阵乘法是种极其耗时的运算.以C = AB为例,其中A和B都是 n x n 的矩阵.根据矩阵乘法的定义,计算过程如下：

SQUARE-MATRIX-MULTIPLY(A, B)
n = A.rows
let C be a new nxn matrix
for i = 1 to n
    for j = 1 to n
        c[i][j] = 0
        for k = 1 to n
            c[i][j] += a[i][k] * b[k][j]
return C

由于存在三层循环,它的时间复杂度将达到 $O(n^3)$.
Strassen算法运用分治法将两个nXn的矩阵乘积运行时间,从简易矩阵乘法算法 $O(n^3)$提升到 $O(n^{\log 7}) = O(n^{2.81})$.下面是算法的主要思想和步骤.

一般情况下,矩阵乘积C=AB,其中A、B和C都是nXn方阵,假定n是2的幂,把A、B和C划分成四个n/2Xn/2矩阵：

则矩阵乘法对应四个等式：

r=ae+bg
s=af+bh
t=ce+dg
u=cf+dh

每个等式运行包含两次 $n/2 n/2$矩阵乘法和两次乘积所得的 $n/2 n/2$矩阵的加法运算,推出 $n * n$ 矩阵相乘所需时间T(n)的递归式：
$$T(n)=8T(n/2)+ O(n^2)$$

Strassen算法在这个一般性的递归式上,发现只需要进行7次 $n/2 * n/2$矩阵乘法即可解决,即
$$T(n)=7T(n/2)+O(n^2)= O(n^{\log 7}) = O(n^{2.81})$$
具体算法步骤如下：

• 1.输入矩阵A和B划分为 $n/2 * n/2$的子矩阵;
• 2.运行 $O(n^2)$标量加法和减法运算,计算出14个 $n/2 * n/2$的矩阵 $A_1,B_1,A_2,B_2, \dots, A_7,B_7$;
• 3.递归计算出7个矩阵的乘积 $P_i=A_i * B_i,i=1,2, \dots, 7$;
• 4.使用 $O(n^2)$ 次标量加法与减法运算,对 $P_i$ 矩阵的各种组合进行求和或求差运算,从而获得结果矩阵C的四个子矩阵r\s\t\u.

Strassen算法的核心思想是什么呢？何以产生如此一个步骤的算法呢？依据是什么？
设想每个矩阵的积 $P_i$可以写成如下形式：
$$P_i=A_iB_i=(α_{i1}a+α_{i2}b+α_{i3}c+α_{i4}d)( β_{i1}e+β_{i2}f+β_{i3}g+β_{i4}h)$$
其中系数α和β都属于集合{-1,0,1},就是说,对矩阵A和B的子矩阵进行加减运算,并对所得的结果进行相乘法来计算出每个子矩阵的乘积.简单说,将子矩阵的乘法运算变成加减运算,从而将8次乘法减少到7次.这是Strassen算法的核心思想和依据.

上面给出的描述很好理解算法的思路和步骤.正如算法导论中对该算法的讨论中所指出的问题,对于矩阵乘法的困难(多项式时间内完成的算法)是合理的.Strassen算法并不是最佳,但目前并没有更多的突破.

2.求解线性方程组(LUP分解思想)
求解一组同时成立的线性方程式在很多应用中都会出现,也是线性代数的基本问题.可以将一个线性系统表示为一个矩阵方程,其中每个矩阵或向量元素都属于一个域,如实数域R.
n个未知量的n个方程用矩阵表示如下：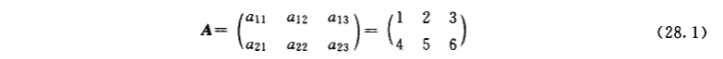

设 $A=(a_{ij}),x=(x_i),b=(b_i)$,有Ax=b.

如果A是非奇异矩阵(秩为n),存在逆矩阵 $A^{-1}$,则 $x= A^{-1}b$,且x是唯一解.方程数目少于未知量数目(或A的秩小于n)为不定方程组,具有无穷多解,如果方程组不相容则可能无解;方程数目多于未知量数目为超定方程组,可能无解.
LUP分解在求解线性方程组具有数值稳定和速度快的优点.LUP分解的思想就是找出三个n*n矩阵L、U和P,满足PA=LU,其中L是一个单位下三角矩阵、U是一个上三角矩阵、P是一个置换矩阵.

定义y=Ux,其中x是要求解的未知向量.用正向替换($O(n^2)$)方法求解Ly=Pb,在用逆向替换($O(n^2)$)方法求解Ux=y,可得：

$$Ax = P^{-1}LUx = P^{-1}Ly = P^{-1}Pb=b$$

问题是如何有效找出LUP呢？只要找出LUP就可以通过正向替换和逆向替换求解x.

LU分解是采用高斯消元法.首先考虑A是nXn的非奇异矩阵,且P等价于$I_n$,找出A=LU,矩阵L和U称为A的LU分解.基于LU分解基础上开展LUP分解,数学基础一致,不失一般性而已,增加对置换矩阵P中值为1的元素的刻画.最重要还是要对矩阵运算和高斯消元法的数据基础有初步掌握.LUP分解如下

lu-decomposition(A)
n <- rows[A]
for k <- 1 to n
    do u{kk} <- a{kk}
        for i <- k + 1 to n
            do l{ik} <- a{ik}/u{kk}
                u{ki} <- a{ki}
        for i <- k + 1 to n
            do for j <- k + 1 to n
                do a{ij} <- a{ij} - l{ik}u{kj}
return L and U

LU分解执行过程如下:

总结:基于LUP分解矩阵求解线性方程组的方法,同样适用于非奇异矩阵的求逆.矩阵乘法和计算逆矩阵问题具有相同难度的两个问题,在一定技术条件限制下可以使用一个算法在相同渐进时间内解决另外一个问题,即可用Strassen矩阵乘法算法来求一个矩阵的逆.

Chapter28 线性规划

怎么样问题可以建模为线性规划来解决呢？在给定的有限的资源和竞争约束情况下,取得最大化或最小化目标的问题.导论中给出政治竞选问题、航空航线调度问题、钻井采油问题.最大化或最小化目标是函数的因变量,自变量就是资源的约束因素,其函数就是由这些制约因素构成的等式或不等式.
1.线性规划定义.

在一般线性规划问题中,最优化一个满足一组线性不等式约束的线性函数.已知一组实数 $a_1,a_2, \dots,a_n$和一组变量 $x_1,x_2, \dots,x_n$,基于这些变量的一个线性函数f定义为
$$ f(x_1,x_2, \dots,x_n) = a_1x_1 + a_2x_2 + \dots + a_nx_n = \sum_{j=1}^n a_jx_j$$
如果b是一个实数而f是一个线性函数,则等式：
$f(x_1,x_2, \dots,x_n) = b$ 是一个线性等式.
$f(x_1,x_2, \dots,x_n) \leq b$ 和 $f(x_1,x_2, \dots,x_n) \geq b$ 是线性不等式.
线性约束就是函数f和b的关系,就是求解n个变量m个线性不等式的最大化,约束为线性不等式的线性函数最大化称为标准型;而约束为线性等式的线性函数的最大化称为松弛型.

基于上面描述可知,线性规划问题是要最小化或最大化一个受限于一组有限的线性约束的线性函数.最小化线性规划和最大化线性规划的分类,是基于目标的需求,同样是m个线性不等式约束,去求解n个变量的值,达到目标(最大化或最小化).

2.凸形区域定义：
区域内的任何两点之间连线上的点都属于这个区域.
线性规划中,二维空间(两个变量)所构成的凸形区域为可行区域,要最大化的函数为目标函数.可行区域内的每个点都会去评估目标函数$x_1+x_2$,将目标函数的一个特点点上的值称为目标值,识别出一个有最大目标值的点就是最优解.当然有二维线性规划不等式所构成的可行区域上是有无数个点,不可能都去求值,因此需要找出一个有效的方式来寻找最大目标值的点.线性规划的最优解必定是在可行区域的边界上,所以只要沿着边界寻找顶点就可以很快找到最大目标值的点.
推而广之,如果有三个变量,则每个约束以三位空间的一个半空间来描述,三个半空间的交集构成了可行区域,目标函数取目标值的点集合是一个平面.因为可行区域也是凸的,取得最优目标值的点集合必然包含可行区域的一个顶点.延伸到n个变量的超平面,每个约束定义了n维空间中的一个半空间,这些半空间的交集形成的可行区域称作单纯形,目标函数是一个超平面,且是凸性,一个最优解也是在单纯形的一个顶点上取得.理解下,无论多少维,找出凸形区域,目标函数的最优解就是在凸形区域的顶点集合之一或多个.

3.单纯型算法
单纯形算法输入一个线性规划(n个变量m个线性不等式),输出一个最优解.算法从单纯形的某个顶点开始,执行一系列迭代,每次迭代中,沿着单纯形的一条边从当前顶点移动到一个目标值不小于当前顶点的相邻顶点.当达到一个局部最大值,即一个顶点的目标值大于其所有相邻顶点的目标值时,算法终止.因为可行区域是凸的且目标函数是线性的,所以具备最优事实就是全局最优的.

单纯形算法需要指数时间.线性规划的第一类多项式时间算法是椭圆算法,运行缓慢;第二类指数时间的算法是内点法,在大型输入上,性能优于单纯形算法.如果在线性规划中,所有的变量都取整数值,即整数线性规划,对于该问题,找出一个可行解是NP难度的.目前还没有已知的多项式时间算法能NP难度问题,所以没有有效的整数线性规划多项式时间算法.当然,一般的线性规划可以在多项式时间内解决.

线性规划的关键步骤:
1.标准型/松弛型转化
标准型的线性规划所有的约束条件都是不等式,而松弛型中的约束是等式.要用单纯形算法求解线性规划,需要将所有线性规划转化为标准型,再将标准型转化为松弛型,线性方程组等式求解.
标准型定义：
已知n个实数 $c_1,c_2, \dots,c_n$;m个实数 $b_1,b_2, \dots, b_m$;以及m * n个实数 $a_ij,其中i=1,2,\dots, m,而j=1,2, \dots, n$ 希望找出n个实数$x_1,x_2, \dots, x_n$来最大化目标函数：
$$ \sum_{j=1}^n c_jx_j$$
满足n + m个不等式, 其中n个约束为非负性约束:
$$ \sum_{j=1}^n a_{ij}x_j \leq b_i, i = 1,2, \dots, m
x_j \geq 0, j= 1, 2, \dots, n$$
用矩阵表示更紧凑：
$$最大化c^Tx,满足约束：Ax \leq b,x \geq 0$$

满足所有约束的变量 $x_s$设定为可行解,而不满足至少一个约束的变量 $x_s$ 设定为不可解.称一个解xs拥有目标值 $c^Tx_s$,在所有可行解中其目标值最大的一个可行解 $x_s$是一个最优解,称其为目标值 $c^Tx_s$的最优目标值.如果一个线性规划没有可行解,则称此线性规划不可行,否则是可行的.如果一个线性规划有一些可行解但没有有限的最优目标值,则称此线性规划是无界的.
已知一个最小化或最大化的线性函数受若干线性约束,总可以将这个线性规划转换为标准型.换句话说,要将非标准型的线性规划转化为标准型的.为什么会有非标准型的线性规划呢？可能目标函数是一个最小化而不是最大化;可能拥有的变量不具有非负性约束;可能有等式约束;可能有大于等于的不等式约束,而不是小于等于.
将非标准的线性规划转化线性规划,最重要是确保转换后的线性规划最优解也是转换前的线性规划最优解,转化前后的两个线性规划是等价的.转化思路就是对目标函数系数取负,并将不具有非负约束性的变量转换成具有非负性约束的变量.

为了利用单纯形算法高效地求解线性规划,需要将标准型转换成松弛型,就是非负约束是不等式,其他约束都是等式.转换思路就是利用松弛变量,就是将不等式的余量用s来接收,从而使不等式变成等式,形式如下：
$$目标函数: z = v + \sum_{j=1}^n c_jx_j \\
约束条件(不含变量的非负性约束: b_i - \sum_{j=1}^n a_{ij}x_j = x_i$$
基于松弛型线性规划,就可以用单纯形算法求解.

2.将问题表达为线性规划：建模
既然定义了线性规划,也知道线性规划可以在多项式时间内求解,那么对于现实的问题,那些事如果形式化为线性规划的问题来求解呢？这就涉及到建模了,现实中的问题如何建模为线性规划来求解.建模：将问题转化成数学形式来求解.

算法导论中对单源最短路径变形的单对最短路径、最大流以及最大流变形的最小费用流和多商品流形式化为线性规划.这里描述下单源最短路径的线性规划形式化

在单对最短路径问题中,已知一个带权有向图G=(V,E),加权函数w:E->R将边映射到实数值的权值、一个源顶点s、一个目的顶点t,要计算从s到t的一条最短路径的权值d[t].将该问题用线性规划表示,要确定变量和约束的集合.在Belleman-Ford算法终止时,对每个顶点v,都一个值d[v],使得每条边 $(u,v) \in E$,有 $d[v] \leq d[u]+w(u,v)$.源顶点初始得到一个值d[s]=0,如此有计算从s到t的最短路径权值的线性规划：
最大化：d[t]
满足约束：$d[v] \leq d[u]+w(u,v)$,对每条边 $(u,v) \in E$成立d[s]=0
共有|V|个变量d[v],每个顶点v∈V各有一个,有|E|+1个约束,每条边各有一个再加上源顶点d[s]=0的额外约束.

3.单纯形算法实现
单纯形算法是求解线性规划的古典方法.单纯形算法和高斯消元法迭代原理类似,高斯消元法是从解未知的一个线性等式系统开始.可以将单纯形算法看成是线性不等式系统上的高斯消元法.单纯形算法的迭代主要思想是：从线性规划的松弛型中得到每次迭代关联的基本解,将每个非基本变量设为0,并从等式约束中计算基本变量的值;一个基本解对应于单纯形的一个顶点;代数上,一次迭代将一个松弛型转换成一个等价的松弛型;相应的基本解的目标值不小于前一次迭代中的目标值,要实现迭代过程中目标值的递增,要选择一个非基本变量作为指示变量,从0开始增加这个变量的值,和目标值一起增加,增加到某个基本变量变为0为止再重写松弛型,将这个基本变量和所选的非基本变量进行角色互换,就是重写线性规划直到最优解很明显.

单纯形算法主要关键是主元选择,并且有三个关键点:

• 1.确定线性规划是可行的;
• 2.确定线性规划是具有可行解而不是无界;
• 3.主元如何选择换入变量和换出变量.

主元选择算法如下:

pivot(N, B, A, b.c. v, l, e)
#compute the conefficients of the equation ofr new basic variable x
b{e} <- b{l}/a{le}
for each j in N - {e}
    do a{ej} <- a{lj}/a{le}
a{el} <- 1/a{le}
#compute the conefficients of the remaining constraints
for each i in B - {l}
    do b{i} <- b{i} - a{ie}b{e}
    for eahc j in N - {e}
        do a{ij} <- a{ij} - a{ie}a{ej}
    a{il} <- a{ie}a{el}
#compute the objective function
v <- v + c{e}b{e}
for each j in N - {e}
    do c{j} <- c{j} - c{e}a{ej}
cl{e} <- -c{e}a{el}
#compute new ses of basic and nonbasic variables
N = N - {e} union {l}
B = B - {l} union {e}
return (N, B, A, b, c, v)

对标准型的输入来求解最优解的算法描述如下:

simple(A, b ,c)
(N, B, A, b, c, v) <0 initialize-simple(A, b, c)
while some index j in N has c{j} > 0
    do choose an index e in N for which c{e} > 0
        for each index i in B
            do if a{ie} > 0
                then delta{i} <- b{i}/a{ie}
                else delta{i} <- INT
            choose an index l in B that minimizes delta{i}
            if delta{i} = INT
                then return "unbounded"
                else (N, B, A, b, c, v) <- pivot(N, B, A, b, c, v, l, e)
for i <- 1 to n
    do if i in B
        then x{i} <- b{i}
        else x{i} <- 0
return (x{1}, x{2}, ..., x{n})

这里一般性地理解下,要通过单纯形算法来求解,在算法之前要肯定线性是可行(单纯性算法最初有一个初始化过程,会判断线性规划是否可行,返回一个初始基本解可行的松弛型),在算法之中要确保不陷入退化或说循环(目标值越迭代越小),能够终止返回最优解.单纯形算法输入一个标准型线性规划,返回线性规划一个最优解,能够顺利找到最优解并终止算法,后续对偶型可以说明.

一个典型的单纯形算法例子：

首先初始化标准型线性规划,返回一个初始基本解可行的松弛型,或者返回这个线性规划不可行,推出算法;其次对松弛型线性规划开始主元操作,选择非负系数最紧约束的换出变量,和换入变量交换,得到新的线性规划(和原来的线性规划是等价的);不断迭代这个过程,直到最优解确定,并终止返回一个最优解.
对于松弛型线性规划通过主元操作生成的新线性规划,二者是等价的.现在很重要的就是主元操作迭代,是如何选择换出变量的.选择一个在目标函数中系数为正值的非基本变量,尽可能增加其值而不违反任何约束.现在通过一个例子来理解单纯形算法的过程.

1.标准型线性规划转化为松弛型线性规划
标准型：
最大化：
3x1+x2+2x3
满足约束：
x1+x2+3x3≤30
2x1+2x2+5x3≤24
4x1+x2+2x3≤36
x1,x2,x3≥0

松弛型：
最大化：
z=3x1+x2+2x3
满足约束：
x4=30-x1-x2-3x3
x5=24-2x1-2x2-5x3
x6=36-4x1-x2-2x3

确定基本解：把等式右边的所有变量设为0,可得基本解(x1,x2,x3,x4, x5, x6)=(0,0,0,30,24,36),目标值z=0;

2.主元操作迭代第一次,选择增加x1的值.当增加x1值时,x4, x5, x6的值随之减小,但每个变量都有非负约束,所以不能减小到负值,这个时候就要在约束函数上选择最紧约束(就是选择最小增加值).
如果x1值增加到30,那么x4是负值;增加到12,则x5是负值;增加到9,则x6是负值;这个就知道了,9是x1值所能增加的最大值,就是最紧约束,对约束函数x6=36-4x1-x2-2x3互换变量x1和x6的角色,得到：x1=9- x2/4- x3/2- x6/4,代入原线性规划据此可得新的松弛型线性规划,如下：
最大化：
z=27+x2/4+ x3/2- 3x6/4
满足约束：
x1=9- x2/4- x3/2-x6/4
x4=21-3x2/4-5x3/2+x6/4
x5=6-3x2/2-4x3+x6/2
确定基本解,同样把等式右边的所有变量设为0,可得基本解(x1,x2,x3,x4, x5, x6)=(9,0,0,21,6,0),目标值z=27;

3.主元操作迭代第二次,选择增加x3的值,最紧约束是x5=6-3x2/2-4x3+x6/2,最大增加到3/2,否则x5的值为负,和第一次迭代一样,互换x3和x5并代入线性等式获得新的线性规划,可得基本解(x1,x2,x3, x4, x5,x6)=(33/4,0,3/2,69/4,0,0),目标值z=111/4;
第四：主元操作迭代第三次,互换x2和x4并代入线性等式获得新的线性规划,可得基本解(x1,x2,x3, x4, x5,x6)=(8,4,0,18,0,0),目标值z=28,为最优解,(x1,x2,x3)=(8,4,0).
最关心的问题还是具有可行解的线性规划经过这样的迭代,在算法终止时是否确实能找到最优解,这个就留给线性规划对偶性来说明.

4. 单纯形算法分析
   现在我们知道单纯形算法可以在多项式时间内求解线性规划最优解,那么关心两点：

• 是算法终止时,获得的是最优解,这个就是对偶性要回答;
• 二是输入一个线性规划要判断出是可行可解的,这个就是辅助线性规划要回答的.
  任何线性规划都可能是不可行的,或是无界的,或有一个优先目标值得最优解,针对这些个情况,单纯形算法要能正确识别.

线性规划的基本定理：
以标准型给出任意的线性规划L可能是以下三者之一：
第一：有一个有限目标值的最优解;
第二：不可行;
第三：无界;

如果L是不可行的,单纯形算法在初始化中就会返回不可行;如果L是无界的,单纯形算法返回无界,无界就是找不到最优解或者有无限个目标值;当然,满足第一情况的,就会返回有限目标值的最优解.
单纯形算法在初始化过程中,会确定线性规划是否有可行解,如果有,则给出一个基本解可行的松弛型线性规划.这个初始化过程其实就是对线性规划测试可行解.那么是如何来确认存在可行解呢？通过构造辅助线性规划,这个辅助线性规划,比较容易找到一个基本解可行的松弛型.只要辅助线性规划有可行解,则要输入的线性规划也就有可行解.如果线性规划L没有可行解,则初始化返回不可行,否则返回一个基本解可行的合法松弛型.怎么构造辅助线性规划呢？

辅助线性规划：令L是一个标准型的线性规划,令 $L_{aux}$是带有n+1个变量的线性规划：
最小化：-x0
满足约束：
$$ \sum_{j-1}^{n} a_{ij}x_j - x_0 \leq b_i, i = 1, 2, \dots, m \\
x_j \geq 0, j = 0, 1, \dots, n
$$
则当且仅当 $L_{aux}$的最优目标值为0时,L是可行的.
辅助线性规划,增加一个x0变量,并且令目标值为0.对辅助线性规划求解可行解,也是按照主元操作,将标准型转换成松弛型后不断交换变量迭代.辅助线性规划较容易找到可行解.算法导论中证明了辅助线性规划存在可行解就是要求解的线性规划存在可行解.

现在我们要引进线性规划对偶性的概念.对偶性有一个很重要的性质：在一个最优化问题中,一个对偶问题的识别总是可以在一个多项式时间内发现.对偶性是用来证明某个解确实是最优解.还是动态规划思想：已知一个最大化问题,定义个相关的最小化问题,来让着两个问题有相同的最优目标值.如最大流问题的最大流最小割原理.对偶的字面意义,就是我的解也是你的解,大问题的解是小问题的解.

已知一个目标是最大化的线性规划,制定一个对偶线性规划,其目标是最小化,而且最优值与原始线性规划相同.给定一个标准的原线性规划,定义对偶线性规划为：
$$
最小化: \sum_{i=1}^{m} b_iy_i \\
满足约束: \sum_{i=1}^{m} a_{ij}y_i \geq c_j, j = 1,2, \dots, n \\
y_i \geq 0, i = 1, 2, \dots, m
$$
构造对偶,将最大化改成最小化,将约束右边的与目标函数的稀疏角色互换,并且小于等于号变成大于等于号.在原问题的m个约束中,每一个在对偶问题中都一个对应的变量yi,在对偶问题的n个约束中,每一个在原问题中都一个对应的变量xj.

对偶性能证明最优解主要是两点：

• 原线性规划中的目标函数的系数变成对偶线性规划中约束函数的右边值,原线性规划中的约束函数的右边值变成对偶线性规划中目标函数的系数;
• 原线性规划中每一个约束函数的左边等于对偶线性规划中的一个变量,就是原线性规划中的m个约束函数等于m个对偶线性规划中的变量,反之也是.最后证明了对偶线性规划的最优值总是等于原线性规划的最优值.

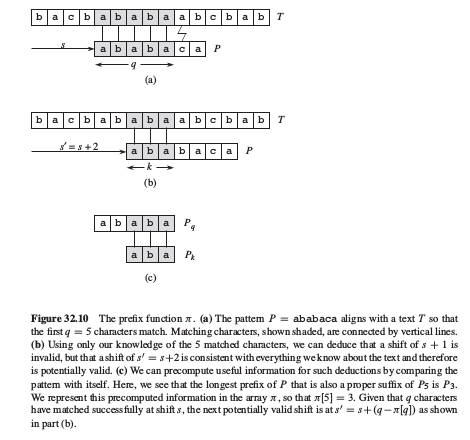
Chapter28 寻找子串

字符串匹配是一个很常见的问题,可以扩展为模式的识别,解决字符串问题的思想被广泛地应用.字符串匹配问题可以描述如下: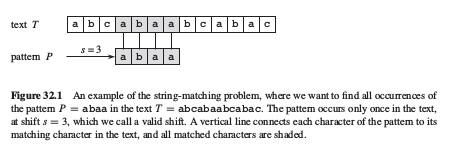

介绍3种解决该问题的办法,包括：最朴素的遍历法,Rabin-Karp算法,自Knuth-Morris-Pratt算法即KMP.
首先对时间复杂度做出一个概括(从大到小)：

• 朴素法：$O((n-m+1)m)$;
• Rabin-Karp：预处理：$O(m)$,匹配：最坏 $O((n-m+1)m)$,但是平均和实际中比这个好得多;
• KMP：预处理O(m),匹配O(n).
  其中,m代表模式P的长度,n代表被匹配的数组S的长度,Σ代表P和S的字符表.

接下来分开学习对应的算法和思想.

1.朴素法(native)

navite-string-matcher(T, P)
n <- length[T]
m <- length[P]
for s <- 0 to n - m
    do if p[1...m] = T[s+1...s+m]
        then print "Pattern occurs with shift"

朴素法简单直接,就是从T的每一个字符开始,看它之后(包括它)的m个字符与P是否一样.P从S中第几个字符开始,可以看作,P在S中位移了几步.
朴素法的效率低的问题在于,它几乎忽视了所有的信息,每一次匹配都是“全新地”.如果P=abc,S=abdabc,从位置0开始,当我们匹配到 位置2,即c != d,朴素的做法是下一步从位置1开始匹配, 然而,在之前的匹配过程中,我们可以知道位置1的值b必然不匹配位置0的a.这是我们光通过P就能知道的,因为既然前一步已经开始去匹配位置2了,证明说明0和1已经成功匹配,而通过P自己,我们知道P的位置1不匹配0,则前一步的S位置1必然也不匹配P的位置1,这样就可以跳过这一步.问题在于,告诉程序跳过多少步,这就是我们接下来的算法要做的.显然,跳过得越多匹配越快,同时我们为了尽可能得到跳步的信息,可能需要进行预处理,预处理会产生另外的时间.

2.Rabin-Karp

rabin-karp-matcher(T, P, d, q)
n <- length[T]
m <- length[P]
j <- d^{m-1} mod q
p <- 0
t{0} <- 0
for i <- 1 to m   #预处理
    do p <- (dp + p[i]) mod q
        t{0} <- (dt{0} + T[i]) mod q
for s <- 0 to n - m  #匹配
    do if p = t{s}
        then if P[1..m] = T[s+1...s+m]
            then print "Pattern occurs with shift"s
        if s <- n - m
            then t{s+1} <- (d(t{s} - T[s+1]h) + T[s+m+1]) mod q

执行过程如下: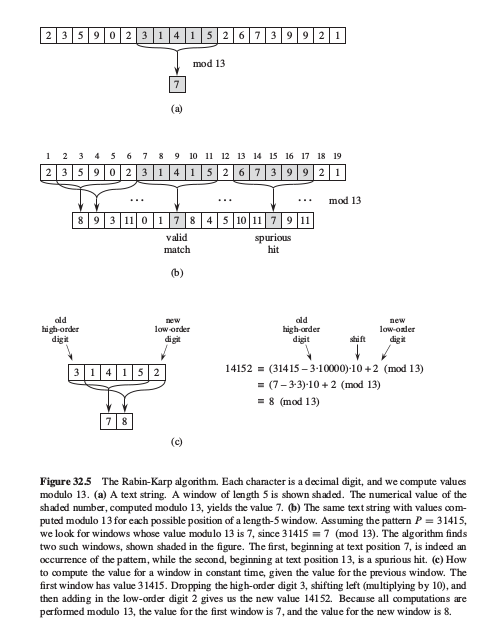

算法将字符串转化为数,进制就是字符表的字符数目.那么,P是一个m位数,这个转化很容易用 $O(m)$ 算出来,通过遍历可以解决.再将S变为n-m+1个数：第一个数同P一样,$O(m)$ 完成预处理;当有了第k个数,算第k+1个数的时候,只需要去掉高位,补上低位,$O(1)$ 完成这个递推过程;总的预处理还是 $O(m)$.匹配的时候就是比较n-m+1次,所以复杂度是 $O(n-m+1)$.那么,为什么说它匹配最坏是 $O((n-m+1)m)$ 呢？
原因在于这个转化得来的数可能很大,算术运算不是常数,怎么处理大数呢？这个时候可以用模除来做一个简单的hash,匹配的数hash一定匹配,hash匹配原数不一定匹配,需要再回去做检查.最差的情况下,所有的hash都一样,每个hash都匹配了,全部需要回去检查一遍,那么这个时候匹配过程和朴素法一样.工程上来说,通常选取一个较大的素数来做模除.算法的最差运行时间是 $O((n-m+1)m)$, 当素数比模式P长度大很多时,期望运行时间是 $O(n+ m)$.

3.KMP
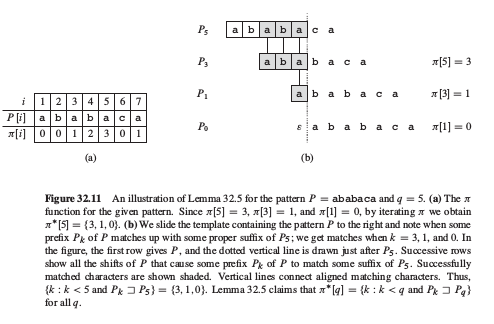
KMP实际上是利用自动机的思想,但是我们并不是预先算好变迁函数.KMP遇到新字符,如果匹配当然是下一个状态,不匹配的话并不像自动机一步到位地接收新字符后到另一个状态,而是先到另一个状态,再递归地看是否接收这个字符,最终接收后在看下一个字符.关键在于,不匹配时,改变状态时是带着新字符还是不带.那么辅助的数组(数组也好,函数也好,总归还是查表),就从多维降到一维,多维是因为自动机遇到不同新字符跳到不同的状态,一维是KMP遇到新字符不匹配时直接跳到另一个状态,跳的时候不考虑新字符.直观上看,构建这样的数组也不再需要遍历Σ,预处理过程复杂度应该会降低.事实,确实省去了O(|Σ|)的复杂度,降到O(m)复杂度.同时,匹配时的复杂度还保持在了O(n).分析复杂度用到平摊分析法.
匹配过程是简单直观的,如前所述,遇到新字符,借助辅助数组π不断地改变状态.伪代码乳如下：

kmp-matcher(T,P)
n <- length[T]
m <- length[P]
π <- kmp-computer-prefix(P)
q <- 0               // state , number of char matched
for i <- 1 to n
    while q > 0 && P[q+1] != T[i]  // P and T range from 1 to n, not 0 to n-1
        do q <- π[q]
        if P[q+1] = T[i]
            then q <- q+1
        if q = m
            then print "Pattern occurs with shift" i-m
                q <- π[q]

那么,问题的关键还是在于计算辅助数组π,即状态如何转移.这里KMP计算的时候,从P的低位(左边)开始计算π,显然只会用到前面低位的信息,不会用到后面高位的信息.那么利用动态规划中利用记录减少迭代的思想,再把计算π的过程看做与匹配过程类似,比如计算q+1那么就是用Pq去匹配Pq+1嘛,而Pq的数组π已经建立好了.

kmp-computer-prefix(P)

m <- length[P]
π[1] <- 0
k <- 0               // just like q above, number of char matched
for q <-  2 to m     // like i above, and actually it is state, so its name is q
    while k>0 && P[k+1] != P[q]  // P range from 1 to n, not 0 to n-1
        do k <- π[k]
        if P[k+1] = P[q]
            then k <- k+1
        π[q] <- k
return π

kmp算法执行如下: