introduction to algorithms note5

发表于

＜Introduction to algorithms＞笔记

Part6 图算法

在前面的部分学习了表示一对一关系的线性数据结构(数组, 链表, stack, queue), 表示一对多关系的树型数据结构(二叉树, 森林, 堆)后, 将其拓展到多对多关系-图.在part6主要是学习用图定义的计算问题和对应的算法,主要包括三个部分:

  • 图的表示,及广度/深度优先的图搜索算法
  • 求解最小生成树问题
  • 最短路径问题

约定:以 $G = (V, E)$ 描述一个图G, 其顶点集为V[G], 顶点数为|V|;边集为E[G], 边数为|E|;故图问题的输入规模的参数有两个, |V|和|G|.例如,算法的复杂度为 $O(VE)$ 表示该算法的运行时间的 $O(|V||E|)$

Chapter22 如何表示和遍历图?

本章的图搜索技术是图算法领域的核心.分为五个部分:

  • 图的表示
  • 广度优先搜索
  • 深度优先搜索
  • 有向无环图的拓扑排序
  • 有向图的强连通子图

图的表示

两种基本的表示方法:

  • 邻接表(adjacency lists)
    包含|V|个链表的数组Adj表示, 对 $u \in V$, 有Adj[u] 包含图G中和顶点u相邻的所有顶点.其适用于稀疏图($|E|远小于|V|^2$).
    不论是有向图还是无向图,邻接表法都有一个很好的特性,即它所需要的存储空间为 $O(V+E)$ ;邻接表表示法稍作修改就能支持其它多种图的变体,因而有着很强的适应性.

  • 邻接矩阵(adjacency matrix)
    G的邻接矩阵为|V| * |V|的矩阵 $A = {a_{ij}}$, 其满足:
    $$ a_{ij} =
    \begin{cases}
    1, \text {if (i, j)} \in E \\
    0, else \\
    \end{cases}
    $$
    适用于稠密图, 空间复杂度 $O(v^2)$
    无向图的邻接矩阵A就是它的转置矩阵,即$A=A^T$ .在某些应用中采用矩阵严肃哦存储,可以只存储邻接矩阵的对角线及对角线以上的部分,这样一来,图所占用的存储空间可以减少一半.

图1 无向图的邻接表和邻接矩阵表示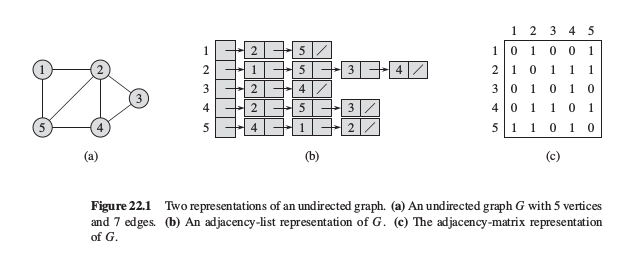
directed graph

图2 有向图的邻接表和邻接矩阵表示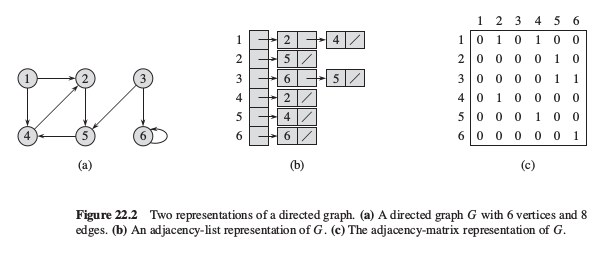
undirected graph

邻接表表示和邻接矩阵表示在渐近意义上至少是一样有效的,但由于邻接矩阵简单明了,因而当图较小时,更多多地采用邻接矩阵来表示.另外,如果一个图不是加权的,采用邻接矩阵的存储形式还有一个优越性:在存储邻接矩阵的每个元素时,可以只用一个二进位,而不必有一个字的空间.这样,当采用了二进位以及表示无向图的技巧时,邻接矩阵法的占用空间大的缺点就可以得到一定程度上的改善.

BFS思路: 给定图G=(V, E)和特定原顶点s, 遍历G中的边, 发现可从s到达的所有顶点, 并计算s到所有可达顶点间的距离(最少的边数).因为始终是将已发现顶点和未发现顶点之间的边界沿广度方向扩展,即首先遍历和s距离k的顶点, 然后发现和s距离k+1的顶点.
BFS实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
BFS(G, s)
for each vertex u in V[G]-{s}
    do color[u] <- white      #color数组:标记是否访问并可视化算法
        d[u] <- INT           #d[u]: u到源点s的距离
        f[u] <- Null          #f[u]: u的父顶点
color[s] <- gray
d[s] <- i
f[s] <- Null
Q <- Empty                     #Q:先进先出队列
Enqueue(Q, s)
while Q != Empty
    do u <- Dequeu(Q)
    for each v in Adj[u]
        do if color[u] = white
            then color[u] <- gray
            d[v] <- d[u] + 1
            f[v] <- u
            Enqueue(Q, v)
    color[u] <- black

算法过程如图3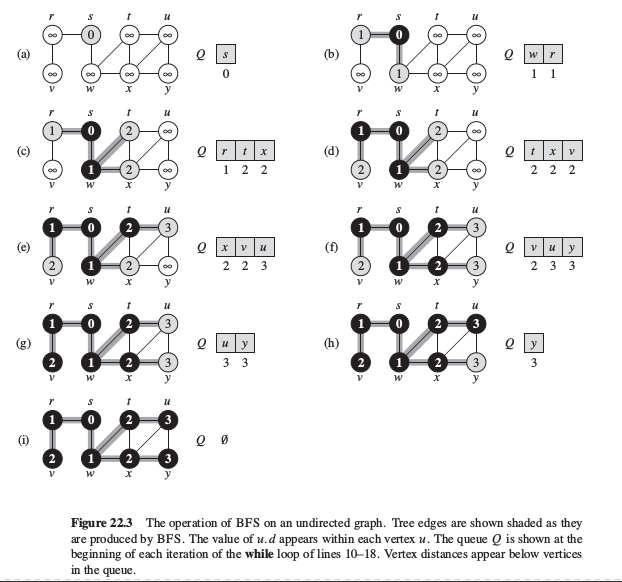
BFS

BFS分析:
采用part4学习的聚集分析(aggregate analysis), 通过color数组的染色标记,确保每个顶点v只Enqueue一次,故亦只Dequeue一次.Enqueue和Dequeue要求 $O(1)$ 的时间,故队列操作时间为 $O(V)$.又有每个顶点v出队时扫描其邻接表Adj[v], 所以每个顶点邻接表只遍历一次, 花费时间为 $O(E)$. 故总运行时间为 $O(V + E)$.

将BFS理解为同心圆扩展算法, 想象图G为一片水面, 源点s就是我们扔进石子的点, 激出的波纹沿半径方向延伸,圆圈向外扩展的过程即是遍历水面的过程.在这个过程中,BFS构造了一棵广度优先搜索树,包括s的所有可达顶点.对从s可达的任意顶点v,广度优先树中s到v的路径对应于图G中s到v的一条最短路径(边数最少).从BFS的算法中的数组f[u]可以用前驱图子图 $G_f = (V_f, E_f)$ 表示图G = (V, E)的广度优先树:
\begin{align}
V_f = {v \in V: f[v] \neq Null } \bigcup {s} \\
E_f = {(f[v], v): v \in V_f - {s} }
\end{align}

根据BFS算法用递归输出s到v的最短路径如下:

1
2
3
4
5
6
7
print-path(G, s, v)
if v == s
    then print s
    else if f[v] = Null
        then print "no path from" s "to" v "exists"
        else print-path(G, s, f[v])
            print v

DFS思路:对新遍历的顶点u, 如果还有以u为起点而未遍历的边,沿此边继续遍历.如果u的所有边都已遍历,则回溯到发现顶点u有起始点的顶点边.制止发现所有顶点为止.可以发现DFS按深度为策略进行遍历.
DFS实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
DFS(G)
for each vertex u in V[G]
    do color[u] <- white
        f[u] <- Null
time <- 0                       #全局计时器, 确定完成时间f[v]
for each vertex u in V[G]
    do if colo[u] = white
    then DFS-visit[u]

DFS-visit(u)
colo[u] <- gray
d[u] <- time + 1
d[u] <- time
for each v in Adj[u]
    do if color[v]  = white
        then f[v] <- u
        DFS-visit(v)
color[u] <- black
f[u] <- time <- time + 1

DFS可视化如图4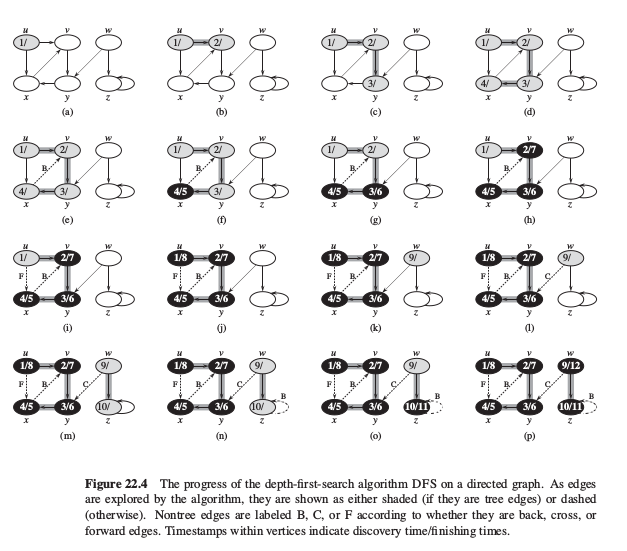
dfs

DFS分析: 仍然采用聚集分析, 每个顶点的邻接表被遍历一次, 要求 $O(V)$.对每个顶点u, 过程DFS-visit仅被调用一次,即只对未遍历的顶点调用该过程.在DFS-visit(v)的一次执行中,遍历的标记过程被执行|Adj[v]|次,且有:
$$ \sum_{v \in V}|Adj[v]| = O(E) $$
故DFS的总运行时间为 $O(V + E)$.

DFS创建一个深度优先森林外,深度优先搜索同时为每个顶点加盖时间戳.每个顶点 v 有两个时间戳:当顶点 v 第一次被发现时,记录下第一个时间戳 d[v],当结束检查 v 的邻接表时,记录下第二个时间戳 f[v].许多基于深度优先搜索的图算法都用到了时间戳,它们对推算深度优先搜索的时行情况有很大的帮助.

拓扑排序 Topological sort

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边 $(u,v) \in E[G]$,则u在线性序列中出现在v之前.通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列.拓扑排序运用在在顶点活动网(Activity On Vertex network,简称AOV网)中,确定活动先后的发生顺序.

一个dag的拓扑排序可以理解为图中所有顶点沿水平线排列而成的一个序列.下面是一个典型的活动安排例子: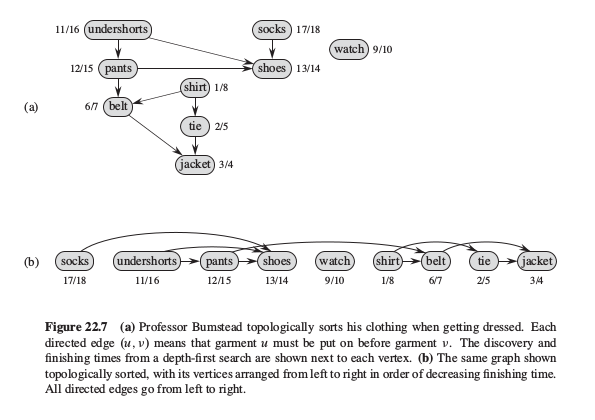
dag

一般由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步,直到不存在入度为0的顶点为止.

  • 选择一个入度为0的顶点并输出之；
  • 从网中删除此顶点及所有出边.
    循环结束后,若输出的顶点数小于网中的顶点数,则输出“有回路”信息,否则输出的顶点序列就是一种拓扑序列.

而在算法导论中运用全局的计时器time,巧妙的实现拓扑排序.通过深度遍历来确定时间完成的时间,按时间顺序自然构造拓扑序列,而无需根据BFS遍历来删除边.

1
2
3
4
topoligical-sort(G)
call DFS(G) to compute finishing times f[v] for each vertex v
as each vete is finished, insert it onto the front of a linked list
return the linked list of vertices

强连通分支

强连通分支(strongly connected component):有向图G=(V,E)的一个最大顶点集合 $C \subseteq V$, 对C中任意一堆对顶点u, v, 它们是互相可达的.

寻找SCC的思路: 定义图G的转置:
$$ G^T = (V, E^T), E^T = {(u, v):(v, u) \in E} $$
对分支图 $G^{SCC} = (V^{SCC}, E^{SCC})$,假设G的强连通分支为 $[C_1, C_2, \dots, C_k]$.顶点集 $V^{SCC} = {v_1, v_2, \dots, v_k }$,对于G的每一个强连通分支 $C_i$,它都包含一个顶点 $v_i$.如果对某个 $x \in C_i$ 以及 $y \in C_i$, G中包含有向边(x, y), 则有一条边 $(v_i,v_j) \in E^{SCC}$. 因此收缩其关联的顶点都处于G的同一强连通分支内的边,即可得到图 $G^{SCC}$. 对应的 $G^{SCC}$是一个有向无环图(dag);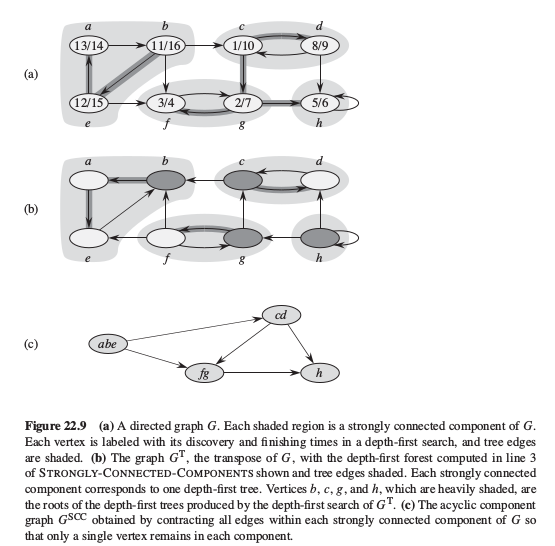
scc

  1. 对G进行深度优先遍历得到每个顶点的时间戳 f[x];
  2. 求得G的返回图 $G^T$;
  3. 按照f[x]的逆向顺序为顶点顺序对$G^T$进行深度优先遍历,即按照G的拓扑排序的顺序对 $G^T$再进行深度优先遍历;
    步骤3得到的各棵子树就是原图 G的各强连通分支.
    1
    2
    3
    4
    5
    strongly-connnected-component(G)
    call DFS(G) to compute finishing times f[u] for each vertex u
    compute GT
    call DFS(GT). but in the main loop of DFS, consider the vertices in order of decreasing f[u](as computed in line 1)
    output the vertices of each tree in the depth-first forest formed in line 3 as a separate strongly connected component

Chapter23 最小生成树 Minimum Spanning Trees

在生成树(spanning tree)T是指: T连接了G的所有顶点且无回路, 因此T必然是一棵树.其中特殊的一类T得到的树的权值最小, 为最小生成树.
采用贪心的思路,可以通过Kruskal算法和Prim算法有效的解决生成树问题.

最小生成树的策略

最小(权值)生成树:由 n-1 条边,连接了所有的 n 个顶点,并且所有边上的权值和最小.一个典型实例如下: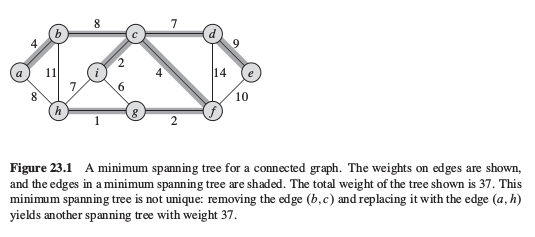
mst

一个通用的贪心策略是,在每个步骤中都形成最小生成树的一条边,算法维护这个集合A, 并保持了以下循环不变式:
每次循环之前, A是最小生成树的一个子集.
在算法的每一步,确定一条边(u, v), 使得它加入集合A后, 循环不变式得以保持, 即 $A \bigcup {(u, v) }$仍然是最小生成树的子集.这样的边(u, v)称为安全边(safe edge).描述如下:

1
2
3
4
5
6
generic-mst(G, w)
A <- Empty
while A does not form a spanning tree
    do find an edge(u, v) that is safe for A
        A <- A union (u, v)
return A

Kruskal算法

Kruskal算法直接基于通用贪心策略:找出森林中连接任意两棵树的所有边中,具有最小权值的边作为安全边,添加其到正在生长的森林中.即,集合A是一个森林,加入集合A中的安全边总是图中连接两个不同连通分支的最小权边.
通过part5高级数据结构中不相交集合可以很好的实现Kruskal算法.比较find-set(u)和find-set(v)是否等同,确定u和v是否属于同一棵树,通过Union实现树的合并.

1
2
3
4
5
6
7
8
9
10
mst-kruskal(G, w)
A <- Empty
for each vertex v in V[G]
    do make-set(v)
sort the edges of E into nondecreasing order by weight w
for each edge(u, v) in E, taken in nondecreasing order by weight
    do if find-set(u) != find-set(v)
        then A <- A union (u, v)
            Union(u, v)
return A

算法可视化如下: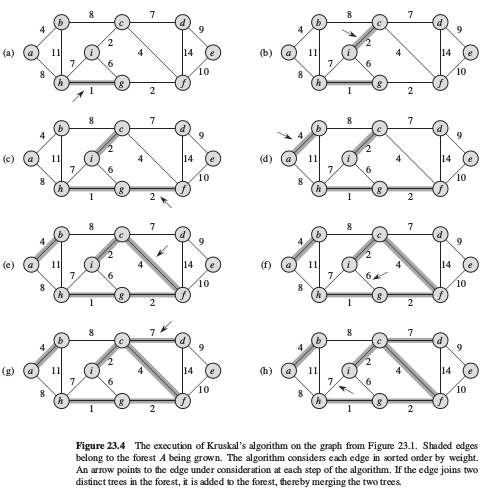
kruskal

Kruskal算法分析:
如果采用不相交数据集合中的按秩结合和路径压缩的策略,可以最高效的实现.初始化要求 $O(1)$, 对各条边排序需要 $O(E\log E)$.对每一条边, 执行 $O(E)$ 次find-set和union操作, 加上|V|次make-set操作,要求的总时间为$O((V + E)\alpha(V)$.假定G是连通的,则有 |E| > |v| - 1, 因而不相交集合操作时间为 $O(E\alpha(v))$. 又有 $\alpha(|V|) = O(\log V) = O(\log E)$,故有总运行时间为 $O(E\log E)$. 由于 $|E| < |V| ^ 2$, 因而 $\log |E| = O(\log V)$, 即Kruskal总运行时间为 $O(E\log V)$

Prim算法

Prim算法的贪心策略:集合A仅形成单棵树,添入集合A中的安全边总是连接树与一个不在树中的顶点的最小权边.树从任意根顶点r开始形成, 每一步里连接了树A与 $G_A=(V, A)$ 中某孤立顶点的轻边(最小权值边)加入到树A中, 直至包含了所有的顶点.如下图: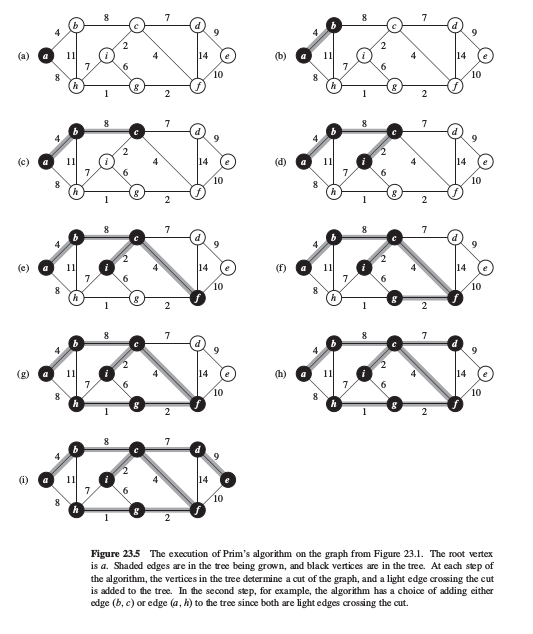
prim

Prim算法维护一个基于key域的最小优先级队列Q,其包含所有不在树A中的顶点.key[u]表示所有与u相连的树中顶点的边的最小权值.f[u]指向u的父节点.

1
2
3
4
5
6
7
8
9
10
11
12
mst-prim(G, w, r)
for each u in V[G]
    do key[u] <- INT
        f[u] <- Null
key[r] <- 0
Q <- V[G]
while Q != Empty
    do u <- extract-min(Q)
        for each v in Adj[u]
            do if v in Q and w(u, v) < key[v]
                then f[u] <- u
                    key[v] <- w(u, v)

Prim算法分析:
Prim算法性能取决于优先队列Q的实现方案, 如果采用Part5学习的二叉堆实现:通过build-min-heao实现初始化, 需要 $O(V)$. while循环体执行|V|次, 每次调用extract-min需要 $O(\log V)$, 故该循环占用时间 $O(V\log V)$.for循环执行 $O(E)$ 次, 每次调用decrease-key实现对key的赋值要求 $O(\log V)$.因此, Prim算法总的运行时间为 $O(V\log V + E\log V) = O(E\log V)$.从渐进意义上来说, Prim算法和Kruskal算法运行时间相同.
如果改进为斐波那契堆, 在Chapter20得到,|V|个元素组成的斐波那契堆,可以在 $O(\log Ｖ)$ 的平摊时间内完成extract-min操作．则Prim算法运行时间可以改进为 $O(E + V\log Ｖ)$.

对比

Prim算法有着更好的实际效率:

  1. Prim算法在执行的过程中,将不在树中的所有顶点都放在一个基于key域的最小优先队列Q中;
  2. 每次在选取安全边时,只需要从Q中弹出最小key值的顶点即可,而不需要像 Kruskal 一样为对所有的边的权值进行一次排序;
  3. Prim 算法使用了用于快速或者最小权值边的技巧(二叉堆、二项堆、斐波那契堆)来加速算法的运行.在最朴素的选取安全边的算法中,需要遍历剩下的所有的边,所需要的时间复杂度为 $O(EV)$,而采用堆来优化后只需要 $O(E\log V)$ ,大大地改善了算法的执行时间(堆的好处).

不过Kruskal算法实现相对简单,所以对于一般的应用Kruskal算法也是可以的．

Chapter24 如何在地图中选择最短的路径?

考虑一个实际问题:在地图上选出从北京到上海的最短距离.直接的想法是北京和上海两点之间的直线, 但实际不可能存在这条路, 北京和上海是通过之间一个个城市中转的.城市抽象为顶点, 城市之间的道路抽象为边,道路里程为权值,则北京到上海的最短路径问题转化为图中的单源最短路径问题.本章即是学习在图中解决最短路径问题的算法

最短路径

定义
给定带权有向图G = (V, E),加权函数 $w: E \to R$从边到实数的映射.
路径 $p = {v_0, v_1, \dots, v_k}$的权为组成边的所有权值之和:
$$ w(p) = \sum_{i=1}^k w(v_{i-1}, v_i) $$
u到v的最短路径的权为:
$$
\delta(u, v) =
\begin{cases}
min{w(p): u \to v }, \text {if path(u, v) exists} \\
\infty, else \\
\end{cases}
$$
对应的最短路径为权 $w(p) = \delta(u, v)$的任何路径.

注:权值是一种度量标准, 不限于距离, 还可以是时间/费用/损失.

问题变体

  • 单终点最短路: 每个顶点v到终点t的最短路, 即将单源最短路问题反向即可
  • 单对顶点最短路: 给定顶点u和v的最短路,u单源最短路的问题选择终点v即可
  • 全源最短路: 找出所有顶点之间的最短路径.

问题分析
1.最优子结构
最短路径的子路径是最短路径.
$$\begin{align}
设路径p = < v_0, v_1, \dots, v_k >是v_0到v_k的最短路径,\
则对 \forall i, j, 1 \leq i \leq j \leq k \
路径p_{ij} = < v_i, v_{i+1}, \dots, v_j>是 v_i到v_j的最短路径 \
\end{align}
$$

2.负权值边
如果问题中存在负权值边, 但不包含负权值回路,则最短路径的定义仍然是正确的.但一旦存在负权值回路, 则不存在最短路径,因为通过不断穿过负权值回路可以得到更小权值的边.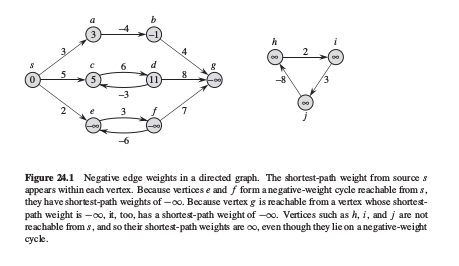
negative path

3.回路
除去负权值回路, 最短路径亦不能包含正权值回路.因为从路径上一出回路后,可以得到源点/终点相同,权值更小的路径.

4.求解路径
最短路径问题中我们不仅想得到最短路径的权,也想得到最短路径是什么.通过类似广度优先搜索树的表示方法,设置顶点v的前驱f[v], 形成最短路径树.然后调用print-path(G, s, v)来递归的输出最短路径即可.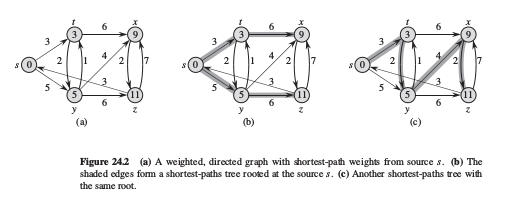
mst-path

5.松弛技术 relaxation
对顶点 $ v \in V$, 设置d[v]描述源点s到v的最短路径权值的上界,初始化如下:

1
2
3
4
5
initialize-single-source(G, s)
for each vertex v in V[G]
    do d[v] <- INT
        f[v] <- Null
d[s] <- 0

松弛操作指, 通过顶点u, 对迄今找到的v的最短路径改进的过程:

1
2
3
4
relax(u, v, w)
if d[v] > d[u] + w(u, v)
    then d[v] <- d[u] + w(u, v)
        f[v] <- u

松弛是最短路径的核心操作, 其是改变最短路径和前驱的唯一方式.本章的算法的区别主要就在对每条边的松弛操作的次数和顺序有所不同.Dijkstra算法对每条边执行一次松弛, 而在Bellman-Ford中执行多次.

Bellman-Ford算法

Bellman-Ford算法运用松弛技术, 对每个顶点, 逐步减小源s到v的最短路径的估计值d[v]直到达到实际最短路径的权.算法返回布尔值,表明图中是否存在从源点可达的负权值回路.实现如下:

1
2
3
4
5
6
7
8
9
bellman-ford(G, w, s)
initialize-single-source(G, s)
for i <- 1 to |V[G]| - 1
    do for each edge (u, v) in E[G]
        do relax(u, v, w)
for each edge(u, v) in E[G]
    do if d[v] > d[u] + w(u, v)
        then return false
return true

可视化如下: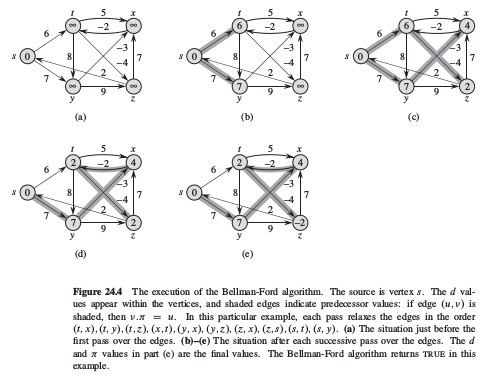
bellman-ford

算法分析:
初始化需要 $O(V)$, 松弛操作的循环共|V| - 1轮, 每轮运行时间为 $O(E)$.检验是否存在负权值回路需要 $O(E)$.故bellman-ford算法的总运行时间为 $O(EV)$.

有向无环图dag中的单源最短路径

按顶点的拓扑顺序对某加权有向无回路图的边进行松弛后, 因为如果存在path(u,v),则拓扑序列中u在v之前.所以在遍历每个顶点时, 只需松弛从该点出发的所有边即可.因此,可以在 $O(V+E)$ 时间内计算出单源最短路径.在一个有向无回路图中最短路径总是存在的,因为即使图中有权值为负的边,也不可能存在负权回路(因为它根本没有任何回路).
实现如下:

1
2
3
4
5
6
dag-shortest-path(G, w, s)
topoligically sort the vertices of G
initialize-single-source(G, s)
for each vertex u, taken in topoligically sorted order
    do for each vertex v in Adj[u]
        do relax(u, v, w)

可视化如下: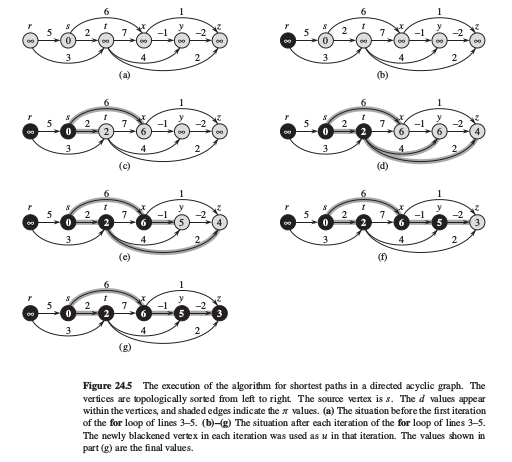
dag-path

Dijkstra算法

Dijkstra算法中设置顶点集合S, 从源点s到集合中顶点的最终最短路径的权值都已确定.其反复选择具有最短路径估计的顶点 $u \in V-S$, 并将u将入S中, 对u的所有出边进行松弛.其中使用了优先级队列Q,来优化顶点d值的选取过程.
实现如下:

1
2
3
4
5
6
7
8
9
dijkstra(G, w, s)
initialize-single-source(G, s)
s <- Empty
Q <- V[G]
while Q != Empty
    do u <- extract-min(Q)
        s <- s union {u}
        for each vertex v in Adj[u]
            do relax(u, v, w)

可视化如下: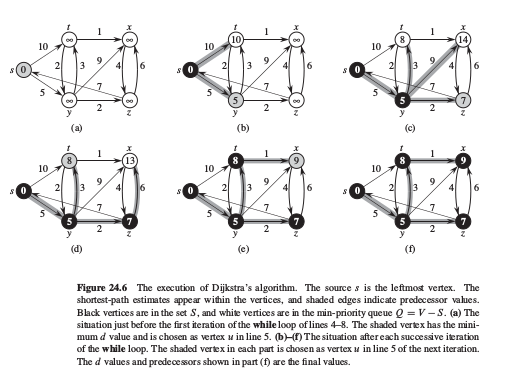
dijkstra

算法分析
dijkstra算法同样依赖优先队列Q的具体实现. 初始化Q调用insert方法 $O(1)$, 每个顶点调用一次, 需要 $O(V)$;for循环共有|E|迭代, 即至多|E|次调用decrease-key $O(1)$,共 $O(E)$.又有每个顶点只加入集合S一次, 故调用extract-min $O(v)$ 共|V|次, 于是dijkstra的总的运行时间为 $O(V^2 + E) = O(V^2)$.
如果采用斐波那契堆实现优先级队列, 因为|V|个extract-min的平摊代价为 $O(\log V)$, 至多|E|个decrease-key操作的每个的平摊代价为 $O(1)$.使得dijkstra算法可以优化到 $O(V\log V + E)$.